CP Physics Ch 7 and 8 notes
MOMENTUM
I. Demo – Two super balls. What is the same before and after collision?
II. Definition
a. What is the difference between a truck and a roller blade?
b. Would you rather be hit by a moving truck or a moving roller blade moving at the same speed?
c. Both the truck and the roller blade are moving masses so they both have momentum = moving mass =
![]()
d. mv = p
e. Which has more momentum?
f. Will the truck always have more momentum? (no, when they are not moving both have 0 momentum)
g. Can they ever have the same non zero momentum? (yes, a very slow moving truck and a very fast moving roller blade!) mV=Mv
III. Impulse
a. Impulse is NOT impact – impact is a force only!!
b. Impulse is the change in momentum which must be caused by a force over time.
![]()
c. Dmv = Ft = J
d. Impulse can be large by increasing the time of the force or using a large force
i. Examples:
1. A long barrel of a cannon designed for long-range projection
2. Pulling your hand backwards when catching a fast ball
3. Jumping into a safety net as compared to concrete pavement
e. Impulse can be small by decreasing the time of the force or using a small force.
i. Examples
1. Jumping into an empty swimming pool
2. Not wearing a seatbelt and hitting the windshield
3. A fast karate chop
f. Why is falling on a wooden floor in a roller rink less dangerous than falling on the concrete pavement? (wooden floor has more give-gives more time for impact force so less change in momentum = less impact force = less pain)
g. Karate and impulse: To increase impact force a karate chop is fast which decreases time, but by pulling back the momentum changes greatly from + to – which increases the total impulse. Since t is small and J is big, F must be REALLY big!
h. Check Q: Would it be better to bounce back from a windshield or go through?
CONSERVATION OF MOMENTUM
I. DEMO – Newtonian balls—what is going on??
II. An external net force is necessary to have an impulse. The net force must be outside the system or momentum is conserved.
III. ‘ means after so that mv = mv’ means the momentum before the collision or explosion is equal to the momentum after the collision or explosion
IV. EXPLOSIONS: this is when the objects are initially at rest, like guns.
a. The initial velocity is therefore 0 and the total momentum of the system is 0
b. This means we have two objects separating after the explosions – m1 and m2 – moving so that the total momentum remains 0. So…
i. m1v1’ + m2v2’ = 0 (but what does that mean about the v’s?)
![]()
ii. m1v1’ =- m1v2’
c. Example:
i. A 50 kg projectile leaves a 2000 kg launcher with a velocity of 400 m/s. What is the recoil velocity of the launcher?
1. G: m1 = 50 kg, m2 = 2000 kg, v1’ = 400 m/s
2. F: v2’ = ?
3. R: m1v1’ =- m2v2’
4.
![]() S:
v2’ = -m1v1’/m2
S:
v2’ = -m1v1’/m2
5. C: v2’ = -(50 kg)(400 m/s)/2000 kg = -10 m/s (- means OPPOSITE so it cancels)
d. STICKY COLLISIONS: Either one or both objects are moving before the collision and they stick together after collision
i. Now both are moving so the equation gets a little bigger
![]()
ii. m1v1 + m2v2 = (m1 +m2)v’
e. Example:
i. A car with a mass of 600 kg travels at 30 m/s and collides with a stationary truck with a mass of 1400 kg. The two vehicles interlock as a result of the collision and slide along the icy road. What is the velocity of the car-truck system?
1. G: m1 = 600 kg, v2 = 30 m/s, m2 = 1400kg
2. F: v’ =?
3. R: m1v1 + m2v2 = (m1 + m2)v’
4. S: v’ = (m1v1 + m2v2)/(m1+m2)
5. C: v’ = ((600 kg)(30 m/s) + 0)/(600 kg + 1400 kg)
= (1800 kg m/s)/ (2000 kg)
![]()
= 9 m/s (in same direction since +)
f. BOUNCY COLLISION: One or both objects are moving before and after the collision.
i. Now things get more complicated
![]()
ii. m1v1 + m2v2 = m1v1’ + m2v2’
g. Example:
i. An offensive and defensive lineman butt heads and bounce off each other. If the offensive lineman is 80 kg and is moving at 10 m/s at the 100 kg defensive lineman who is moving at 20 m/s, and the offensive lineman bounces back at 20 m/s, what velocity does the defensive lineman bounce back at?
1. G: m1 = 80kg, m2 = 100 kg, v1 = 10 m/s, v2 = -20m/s, v1’ = -20 m/s
2. F: v2’ = ?
3. R: m1v1 + m2v2 = m1v1’ + m2v2’
4. S: v2’ = (m1v1 + m2v2 – m1v1’)/m2
5. C: v2’ = ((80kg)(10 m/s) + (100 kg)(-20 m/s) – (80kg)(-20m/s))/(100 kg)
= (800 kg m/s – 2000 kg m/s + 1600 kg m/s)(100 kg)
![]() =
400 kg m/s / 100 kg
=
400 kg m/s / 100 kg
![]()
= 4 m/s backwards from where he came (because its +)
WORK
I. Demo – hanging bowling ball
II. Conservation of Energy
a. Energy is never lost or gained, it is only transformed into another form
b. Forms of energy – heat, motion (kinetic), light, potential (electrical and gravitational)
c. What can energy do? – warm things, move things, hold things still, light things, make things “work”
III. Work
a. Demo – pushing vs sitting in chair, lifting paper vs pushing a nonmoving table (which are work?
b. Formula
i. Work = Force x distance
![]()
ii. W = Fd
iii. ***Force must be in same direction as displacement. Only the component in the direction of d is used in the formula****
iv. Units = Nm = Joule = J (calorie in English system)
c. Check questions –
i. How much work is done lifting a twice-as-heavy barbell the same distance?
ii. How much work is done lifting a twice-as-heavy barbell twice as far?
d. Example:
i. A 2 kg box is pushed with a 4 N force for 3 m, how much work is done?
1. G: m = 2kg, d = 3 m, F = 4 N
2. F: W = ?
3. R: W = Fd
4.
![]() S:
W = Fd
S:
W = Fd
5. C: W = (4N)(3m) = 12 Nm = 12 J
IV. Gravitational Potential Energy
a. Demo:
i. Hold object over head
ii. What happens if I let go?
iii. When it moves, work must be done on it by????
iv. Gravity is there even when my hand is there
v. Therefore,
there is “potential” for doing work due to gravity = Gravitational Potential
Energy = GPE
b.
If I hold the object higher, will it end up falling faster or
slower?...Therefore, more height = more GPE
c.
What force makes it fall? What is the equation for this force?
![]()
d.
Therefore
GPE = mgh
(looks how close this is to W = Fd where F = mg and d = h)
e.
Neglecting friction, does a ball dropped straight down have a
different potential than a ball at the same height on a ramp?
f.
Check questions:
i. A
1000 kg car goes up a ramp that is 200 m high. How much work does it gain? How
much GPE is gained?
ii. G:
m = 1000 kg, h = 200 m, d = 200 m
iii. F:
W = ?, GPE = ?
iv. R:
W = Fd, F = mg, GPE = mgh
v. S:
W = Fd, F = mg, GPE = mgh
vi. C:
F = (1000 kg)(10 m/s2) = 10000 kg m/s2 = 10000 N
![]()
W =
(10000 N)(200 m) = 2000000 Nm = 2 x 106 J
![]()
GPE =
(1000 kg)(10 m/s2)(200 m) = 2 x 106 J
![]()
***So…change in DGPE = DW…don’t
have to compute twice!!***
V.
Kinetic Energy
a.
KE is motion of energy. So what factors would determine how
much motion an object has??
![]()
b.
KE = ½ mv2
![]()
c.
In order to change KE work must be done so that DKE = DW
= Fd
d.
Check questions:
i. Does
a car moving along a road have KE?
ii. If
the speed of the car doubles, by how much does the KE increase?
iii. If
the speed triples?
e.
Example:
i. If
a 1000 kg car starts at rest and achieves a velocity of 40 m/s, how much work
did it gain?
ii. G.
m = 1000 kg, vf= 40 m/s, vi = 0
iii. F:
DW =?
iv. R:
DW = DKE
= ½m(vf2 – vi2)
v. S:
DW = ½mvf2
vi. ![]() C:
DW =½(1000 kg)(40 m/s)2
C:
DW =½(1000 kg)(40 m/s)2
= 800,000 kg m2/s2
= 8 x 105 J
VI.
Power
a.
How fast the work gets done, or the energy is used
![]()
b.
Equation: P = W/t
c.
Units = J/s = watts = w
d.
Can use any J measurement over time
i. Examples:
1.
P = DK/t
2.
P = DGPE/t
CONSERVATION OF ENERGY AND
MACHINES
I.
Conservation of Energy
a.
When you rub two sticks together, what kind of energy is
converted into what kind of energy?
b.
It is important to note that energy is not lost it is only
transferred from one form to another. Energy can NEVER be lost, it just takes
another form
c.
Recall out bowling ball demo, the bowling ball’s potential
energy is converted into kinetic energy but it eventually will slow down and
stop. Where did all the energy go?
II.
Machines
a.
What is a machine? – a device that makes your input
force less (IT DOES NOT DECREASE YOUR WORK)
b.
Machines must obey the law of conservation of energy. That is
you can’t get something for nothing. If I put in less effort (force) and get
more force out, the total energy I put into the machine is the most total
energy I can get out.
c.
The type of energy many machines use is just work, kinetic
energy, and potential energy.
d.
Let’s look at work, W = Fd. So if I put in less F (Fin) and
get out more F (Fout) then in order for Win=Wout (which it must!) what must be
true about din and dout? (dout
< din)
e.
Even more specific…if Fin is half as much as Fout then dout
must be half as much as din. That is, the ratios must be equal.
f.
These ratios have been given names
i. din/dout
= ideal or theoretical mechanical advantage (IMA)
1.
this is the way the machines is designed for an ideal
situation to get the type of machine you want
ii. Fout/Fin
= actual mechanical advantage (MA)
1.
This is the amount the input F is multiplied by the machine in
reality
g.
Remember,
![]()
![]()
i. Win
= Wout and din/dout =
Fout/Fin in IDEAL
situations
ii. Win>Wout
and din/dout>Fout/Fin in REAL
situations
III.
Fin
![]() Three
simple machines
Three
simple machines
a.
Levers
![]()
i. ![]()
 Drawing:
Drawing:
dout din
![]()
![]()
ii. A
lever pivots on a fulcrum so that you must push the lever down a large distance
but this allows you to apply a small force to lift a heavy object
iii. Every
day examples: bottle opener, shovels, arms, legs
iv. Check
question: Archimedes, the most famous scientist in ancient Greece, stated that
if given a long enough lever, he could move the world. What does this mean?
b.
Pulleys – actually type of lever
i. Drawing:
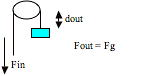
![]()
ii. One
pulley only changes the direction of the force not the amount
iii. With
different pulley configurations, however, the force can be decreased.
iv. DEMO
– Pulleys – measure din and Fin and dout and Fout
v. IMA
is the same as the number of supporting strings
c.
din
![]() Inclined
Planes – ramps
Inclined
Planes – ramps
i. Drawing:
![]()
![]()
ii. Incline
planes are also machines. They allow you to push an object over a large
distance so you can decrease your input force
IV.
Efficiency
a.
Efficiency measures how close a machine is actually being a
PERFECT energy converter.
i. Perfect
= 100% efficient
![]()
ii. Wout/Win
x 100% = e
iii. Can
use ANY energy measurement (J)
1.
Kout/Kin
2.
GPEout/GPEin
3.
MA/IMA
iv. Examples
1.
What is the ideal mechanical advantage of a 5 m long incline
plane with one end elevated to 1 m?
a.
G: din = 5m, dout = 1m
b.
F: IMA = ?
c.
R: IMA = din/dout
d.
![]() S: IMA = din/dout
S: IMA = din/dout
e.
C: IMA = 5m/1m = 5 (NOTICE NO UNITS!)
2.
What is the actual mechanical advantage if 100 N of effort is
needed to push a 400 N block of ice up the plane?
a.
G: Fin = 100 N, Fout = 400 N
b.
F: MA = ?
c.
R: MA = Fout/Fin
d.
![]() S: MA = Fout/Fin
S: MA = Fout/Fin
e.
C: MA = 400N/100N = 4 (NOTICE NO UNITS!)
3.
What is the efficiency of the incline plane?
a.
G: Fin = 100 N, din = 5 m, Fout = 400 N, dout = 1m
b.
F: e = ?
c.
R: e = Wout/Win x 100%, W = Fd
d.
S: e = (Fout)(dout)/(Fin)(din) x 100 %
e.
C: e = (400N)(1m)/(100N)(5m) x 100 %
= 400/500 x 100 %
![]() =
80%
=
80%